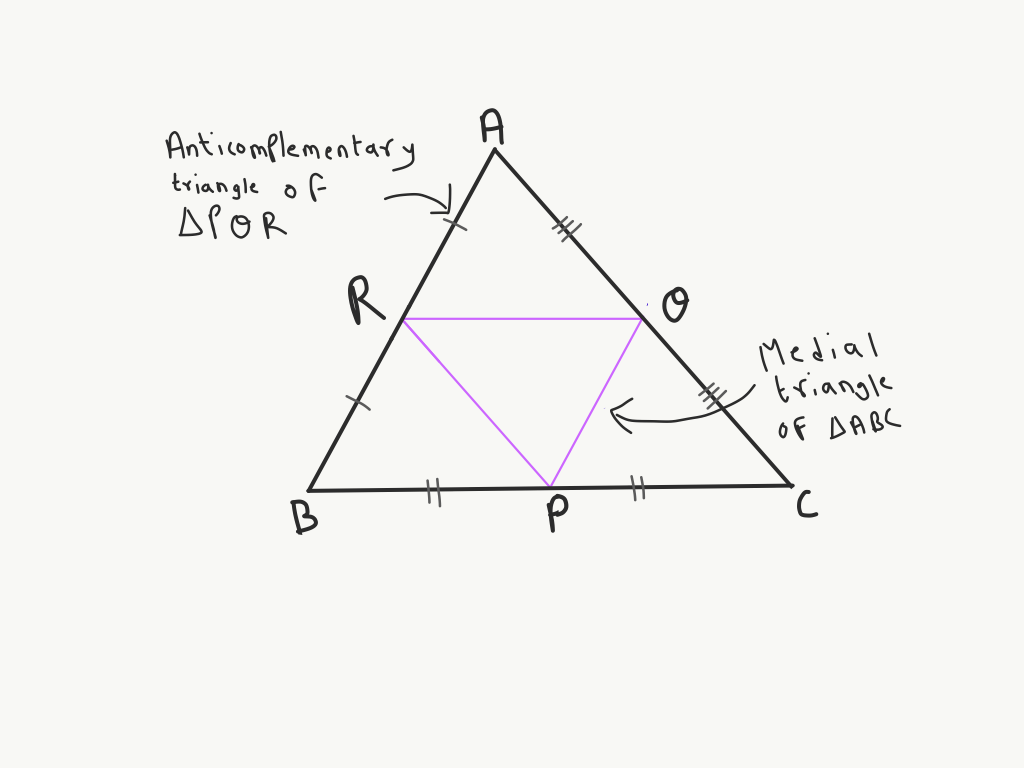
Medial and Anticomplementary Triangles

Let’s take any triangle. We’ll call it the “primary triangle”. Join the midpoints of its three sides with line segments. The result will be a new triangle inside of the primary triangle. This new triangle obtained by connecting the midpoints of the sides of the primary triangle is called the midpoint triangle or medial triangle, not to be confused with the median triangle.

If △PQR is the medial triangle of △ABC, then from the medial triangle’s point of view, the primary triangle △ABC is said to be its anticomplementary triangle. 

△PQR is the medial triangle of △ABC

△ABC is the anticomplementary triangle of △PQR

In an anticomplementary triangle the three midpoints of the sides are the three vertices of its medial triangle. 

Can △PQR have the medial triangle ?

If M, N and O are the three midpoints of the sides of △PQR, then △MNO will be the medial triangle of △PQR. Or we could also say that △PQR is the anticomplementary triangle of △MNO. 

There will also exist a triangle, say △XYZ, whose medial triangle is △ABC. This △XYZ will be called the anticomplementary triangle of △ABC. 

Every triangle has a unique medial triangle associated with it and every triangle has a unique anticomplementary triangle associated with it. 

To avoid confusion between the two types and not to mix them up, maybe it's best to think about each one of them separately with respect to a given or primary triangle. 

• Medial triangle of any given triangle is obtained by joining the midpoints of its sides. 

• If there is a ‘triangle 1’ such that the midpoints of its sides are the vertices of ‘triangle 2’ located inside it, then ‘triangle 1’ is the anticomplementary triangle of ‘triangle 2’.

It happens so that the three sides of a medial triangle are parallel to the three sides of its primary triangle(anticomplementary triangle). This is a famous theorem that goes by the name of Midpoint theorem of triangles(actually, this is just a part of the theorem). 

Here’s a link to my post on a simple two step guide to constructing the anticomplementary triangle in Geogebra - an online graphing calculator.