How to construct Incenter and Incircle in Geogebra

In this post, i will be talking about how to construct the incenter and the incircle of a triangle in Geogebra - an online graphing calculator. 

Incenter is the center of the incircle of a triangle and is very easy to construct. It is also the point where the three angle bisectors of three interior angles of the triangle intersect. We could construct the incenter in Geogebra in the following simple steps(demonstrated with pictures) : 

Read more about the Incenter here.

Step 1 : Drawing a triangle. Select the tool Polygon under the Polygons section in the shapes menu. 

In the graphing panel to the right, click on any three different spots for the three vertices of a triangle. Click again on the first point you made to complete forming the three sided triangle. 

For constructing a triangle of three given side lengths or two given side lengths & one given angle, you can check out this post of mine.

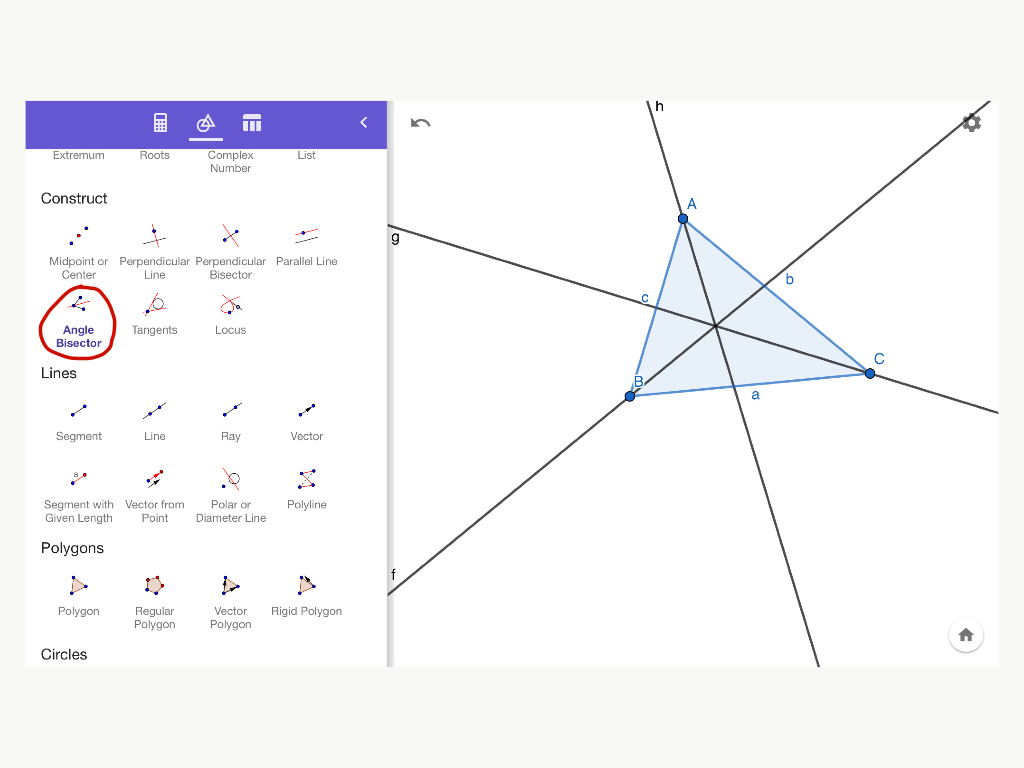
Step 2 : Select the tool Angle Bisector under the Construct Section. 

To construct the angle bisector of an interior angle, say angle B, click on the vertices A... B…and C. Similarly, to draw the angle bisectors of angle C and angle A, click on the vertices A - C - B, and the vertices C - A - B. 

(Note : If instead of the three vertices you would have chosen to click on the two adjacent sides, say AB and BC, the result will be that the two angle bisectors will show up, one for the interior angle B and one for the exterior angle of B. Try it.).

Step 3: So now we know where the location of the Incenter is. To mark this location with a point(dot), select the Intersect tool in the Basic tools section. 

Click on any two of the three angle bisectors. There will appear a point(dot) at the spot where they are intersecting. In the figure above, point D is the Incenter. 

So constructing the incenter was pretty easy. To construct the incircle, we are gonna need this point incenter. But first, what is Incircle? 

There are many ways to describe it. You can think of it as the largest circle that can fit inside the triangle. It “touches” the three sides of the triangle. Or to put it another way, the three sides are three tangents to the incircle. The latter property helps us with the construction.

The three line segments drawn from the incenter to the points of tangencies are the radii of the incircle, and hence equal. Also, these segments are perpendicular to the three sides. 

Step 4 : Select the tool Perpendicular Line under the Construct Section. Click on the point Incenter and any side of your triangle to draw the line perpendicular to that side and passing through the Incenter. Similarly, draw lines perpendicular to the other two sides of the triangle as well as passing through the incenter. 

(For clarity purposes, i have hidden the three angle bisectors in the graph) 

Step 5 : Mark the points where these perpendicular lines are cutting the sides by using the Intersect Tool. They are the points E, F and G in the figure below. 

These are the points at which the three sides are tangents to the incircle. They lie on both the incircle as well on the respective sides. 

Step 6 : Select the tool Circle through 3 Points in the Circles Section. Click on these three points in any order to draw the Incircle of your triangle. And that’s how you draw the incircle after you know where the incenter is located.