Geogebra - Circumcenter & Circumcircle

A circle can be drawn through any three non-collinear points in a 2D coordinate system. If we connect the points with straight segments to form a triangle, the circle will be called the Circumcircle of that triangle, and its center, the Circumcenter. More about it here. 

Circumcenter also happens to be the point where the three perpendicular bisectors of three edges of a triangle intersect. Let’s look at how we can construct the circumcircle and circumcenter in Geogebra - an online graphing calculator. 

To begin with, we need a triangle. I will assume you already know how to construct triangles. But just in case if you don’t, you can check out this post of mine where you will see how to construct triangles with three known side lengths or with two known side lengths & one given angle in Geogebra. Here, i will just go with any casual triangle, which I will construct by using the Polygon tool in the Polygons section. 

You can draw the circumcircle of your triangle using the tool Circle through 3 Points found under the Circles section. Select this tool and simply click on the three points at the vertices. 

Now there is more than one way in which you can construct the circumcenter. One way is simply by finding the center of the circumcircle, just like you would find the center for any circle in Geogebra. It can be easily done using the Extremum tool found under the Basic tools section. 

Select this tool, and click anywhere on the circumcircle. It will return two pairs of diametrically opposite points vertically and horizontally on the circle. We can then choose the tool Midpoint or Center found in the Construct section, and click on any pair of points horizontally or vertically. The point will appear exactly in their middle. That’s the circumcenter, represented by letter H in the picture below. 

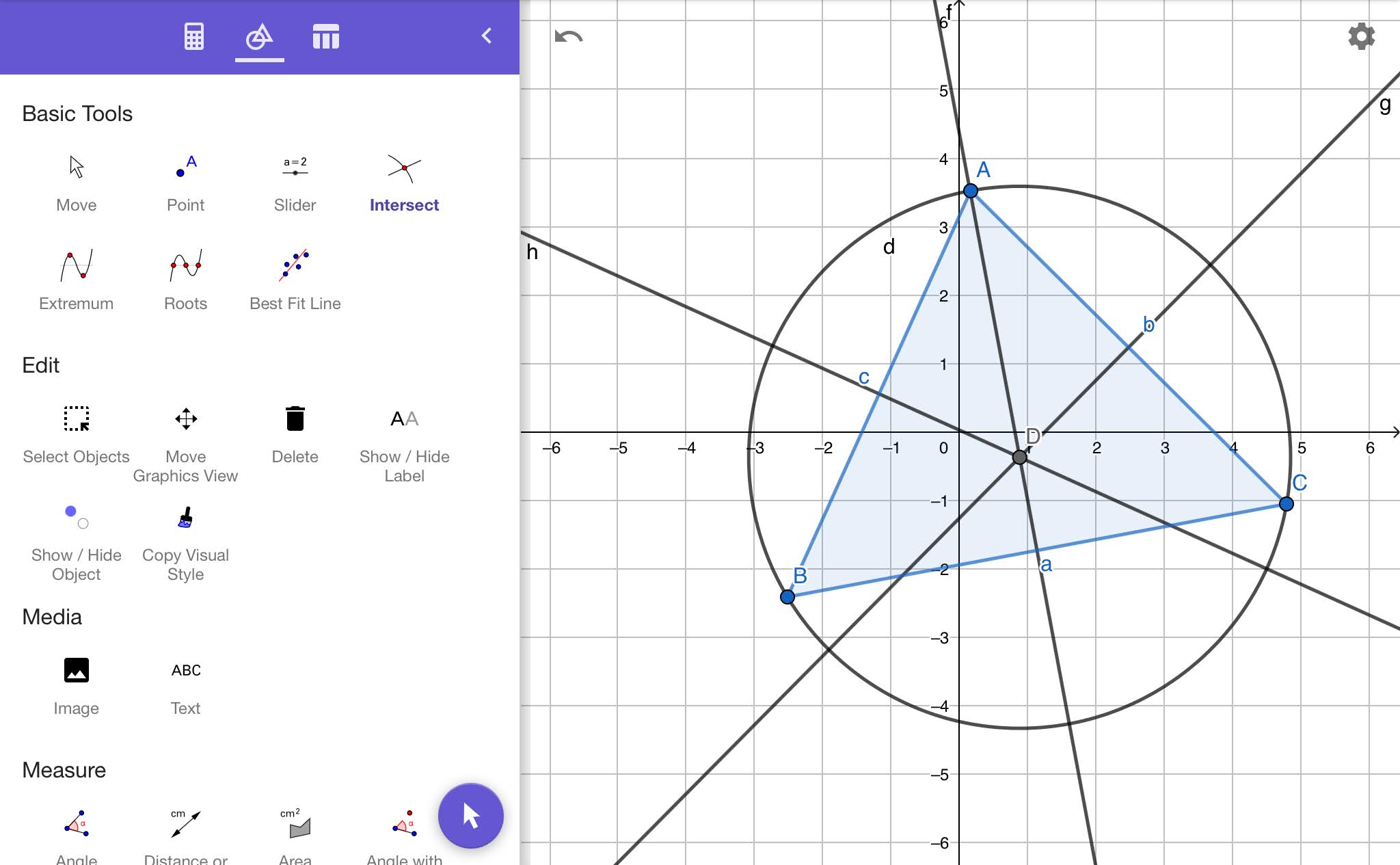
Another way to locate the circumcenter is constructing perpendicular bisectors of three sides. Select the tool Perpendicular Bisector in the Construct section. Simply click on a side to construct its perpendicular bisector. 

To mark the spot at which the perpendicular bisectors intersect with a point, use the Intersect tool in the Basic tools section. Simply click on any two of the three perpendicular bisectors and the point will appear at the location where they are intersecting.