Equation of a line in 3D

In this post I will be talking about how to find vector equation of a line in 3D. 

To find vector equation of a line we need :

• A direction vector of the line

• Coordinates of any point on the line

Equation from direction vector and a point on the line

Direction or directional vector is a vector arrow parallel to the line. Some texts will use the term ‘Direction ratios’ or ‘Direction Numbers’ for direction vector. Direction numbers or direction ratios of a line is a set of three numbers that specify the direction of that line. A line with direction ratios of 1, 2, 3 basically means that \(\hat{i} + \hat{j} + \hat{k}\) is its direction vector, i.e. a vector parallel to that line. 

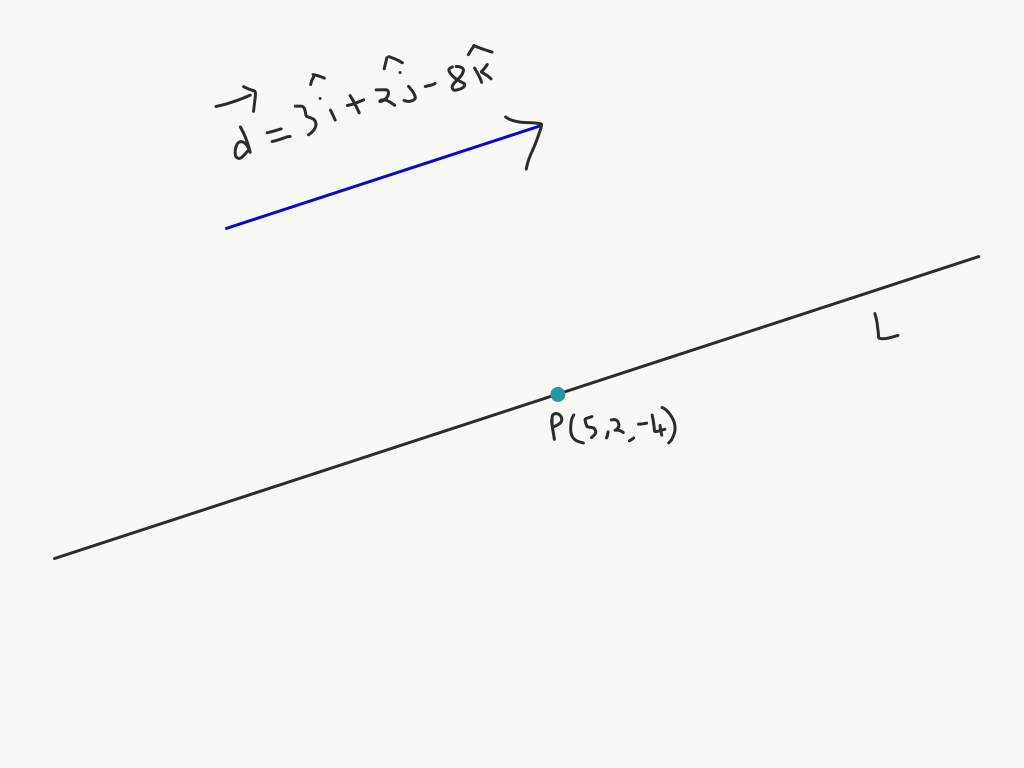
The procedure for finding the equation of a line is simple enough. Consider a line in 3D space; let’s name it L. Suppose \(\vec{d} = 3\hat{i} + 2\hat{j} - 8\hat{k}\) is its direction vector. 

Let P(5, 2, -4) be a point on L. Below is a rough picture of how everything is supposed to look like. 

Define another point Q(x, y, z) on the line. I am calling it a variable point. Its position on the line is not fixed. We are looking for a relation that will tell us how the coordinates (x, y, z) vary as the position of point Q on the line changes, which is just another way of saying that we are looking for an equation of the line. 

The first main step is to define a vector from the given point on the line to the variable point(P to Q), OR.. from the variable point to the given point(Q to P), either way will do. I will go with \(\overrightarrow{PQ}\).

I am calling it a variable vector, its size(length of the arrow) and direction will depend upon where the variable point Q is on the line. But, it is clear that no matter where Q is on L, this vector will always be parallel to the direction vector \(\vec{d}\). It can be either parallel and pointing in the same direction as the direction vector ...OR parallel but going the opposite way. 

In the topic of vectors, we often hear that parallel vectors are scalar multiples of each other. What that basically means is we can enlarge or shrink the size of one vector by the same amount along all three coordinate axes to create a copy of the other parallel vector. 

For example, \(\vec{a}\) & \(\vec{b}\) are parallel vectors as shown below. 

The size of \(\vec{a}\) is one unit in the positive X-direction, one unit in the positive Y-direction and one unit in the positive Z-direction. Clearly, if we increase its size by the same factor of 2 in all three directions, the result will be an exact copy of \(\vec{b}\), which is of the size 2 units in positive x, y and z directions. 

Alternatively, if we reduce the size of \(\vec{b}\) by a factor of ½ along all three axes, we will get a copy of \(\vec{a}\). Note that this will only be true for parallel vectors. 

We write, 

\(\vec{b}\) = 2\(\vec{a}\)

\(\vec{a}\) = ½ \(\vec{b}\)

Number 2 is a scalar, so is ½, the same factor by which we change the size of one vector along all three axes to produce a copy of the other vector. Hence, \(\vec{a}\) & \(\vec{b}\), and generally any two parallel vectors, are said to be scalar multiples of each other. 

If two vectors are parallel but in opposite directions, in that case the scalar factor will be a negative value. 

Going back to our example, since vectors \(\overrightarrow{PQ}\) & \(\vec{d}\) are parallel, there must exist a non-zero scalar c, such that, 

\(\overrightarrow{PQ}\) = c \(\vec{d}\) ….(1)

We could also express \(\vec{d}\) in terms of \(\overrightarrow{PQ}\). In that case, the scalar multiple will be 1/c. 

The size of \(\vec{d}\) is : 3 units along X-axis, 2 units along Y-axis, - 8 units along Z-axis(negative sign because it is in the negative Z-direction). 

For the size of vector arrow \(\overrightarrow{PQ}\) along the three axes, we subtract the coordinates of its tail from the corresponding coordinates of its head. The size of \(\overrightarrow{PQ}\) is then (x - 5) units along X-axis, (y - 2) units along Y-axis, and (z - (-4)) units along Z-axis. 

From (1),

\((x - 5)\hat{i} + (y - 2)\hat{j} + (z + 4)\hat{k}\) = c (\(3\hat{i} + 2\hat{j} - 8\hat{k}\)) …(2)

Also, the size of \(\overrightarrow{PQ}\) along any axis will be c times the size of \(\vec{d}\) along that axis. 

(x - 5) = 3c 

(y - 2) = 2c                ….. (3)

(z + 4) = -8c

(2) is the Vector equation of L. (3) is a three-part Cartesian equation of L . We can combine all parts together by solving for c in all three parts, and then equating them. 

\(\frac{x - 5}{3} = \frac{y - 2}{2} = \frac{z + 4}{-8} = c\)

It is important to note that c is not a constant in the equation, it’s actually a fourth variable. Its value will vary depending on where Q is on the line. 

Let’s check if point Q(3, -4, 0) is on L.

Q will be on L if \(\overrightarrow{PQ}\) is parallel to \(\vec{d}\).  And they will be parallel if there exists a unique c along all three axes such that, 

3 - 5 = 3c  ;  - 4 - 2 = 2c  ;   0 + 4 = - 8c

c = - 2  ;  - 3 = c  ;   c = - 1\2 

We see that c is not the same along all three axes. This means that we will have to scale \(\vec{d}\) by different amounts along three axes to get a copy of \(\overrightarrow{PQ}\). So the vectors \(\overrightarrow{PQ}\) & \(\vec{d}\) are not parallel. Q(3, -4, 0) is not on L. 

Equation from two given points on the line 

You will also encounter problems where a direction vector will not be directly given. Instead, you will be given coordinates of one more point on the line. But that’s not a problem at all. A vector defined from one given point to another given point on the line is nothing but a vector that’s parallel to the line, a direction vector. 

After we have defined the direction vector of the line, we can proceed to finding its equation from its direction vector and any one of the two given points on the line just like we did in the above example.