Finding the Shortest Distance between two Skew Lines

In my previous post on the topic, i clarified that the shortest path between a pair of skew lines is the line segment that is perpendicular to both the skew lines. 

Now the next ask is determining a way to find the length of the shortest path, i.e. the length of the line segment perpendicular to both the skew lines. Let’s take an example of a pair of skew lines.

L1 : $\hat{i}+\hat{j}+0\hat{k}+u(2\hat{i}-\hat{j}+\hat{k})$

L2 : $2\hat{i}+\hat{j}-\hat{k}+v(3\hat{i}-5\hat{j}+2\hat{k})$

From equation of L1, position and direction vectors of L1 are 

$\overrightarrow{p_1}=\hat{i}+\hat{j}+0\hat{k}$

$\overrightarrow{d_1}=2\hat{i}-\hat{j}+\hat{k}$

From equation of L2, position and direction vectors of L2 are

$\overrightarrow{p_2}=2\hat{i}+\hat{j}-\hat{k}$

$\overrightarrow{d_2}=3\hat{i}-5\hat{j}+2\hat{k}$

Direction vector of a line is simply a vector arrow parallel to that line. Or, we can also say it is a vector arrow pointing in any one of the two opposite directions of the line.

The above figure is the graph of the two given lines L1 & L2 along with direction vectors $\overrightarrow{d_1}$ & $\overrightarrow{d_2}$ parallel to L1 & L2. AB is the shortest path perpendicular to both the lines, and we want to find its length. I have created this image using 3D calculator on Geogebra. Below this para, a gif image might provide a little more clearer picture than the static image above. 

Some texts use terms such as ‘Direction Ratios’ or ‘Direction Numbers’ for Direction vector, but all these terms essentially imply the same. For example, 3, -5 and 2 are direction ratios of line L2 basically means that $3\hat{i}-5\hat{j}+2\hat{k}$ is the direction vector of L2 pointing in one of the two directions of L2. 

Position vector of a line is a vector arrow specifying the position of a point on the line relative to the origin, i.e. how much farther away a point on the line is from the origin, and in which direction the point is from the origin. It is an arrow drawn from the origin to the point on the line. A position vector could be given for any point on the line.

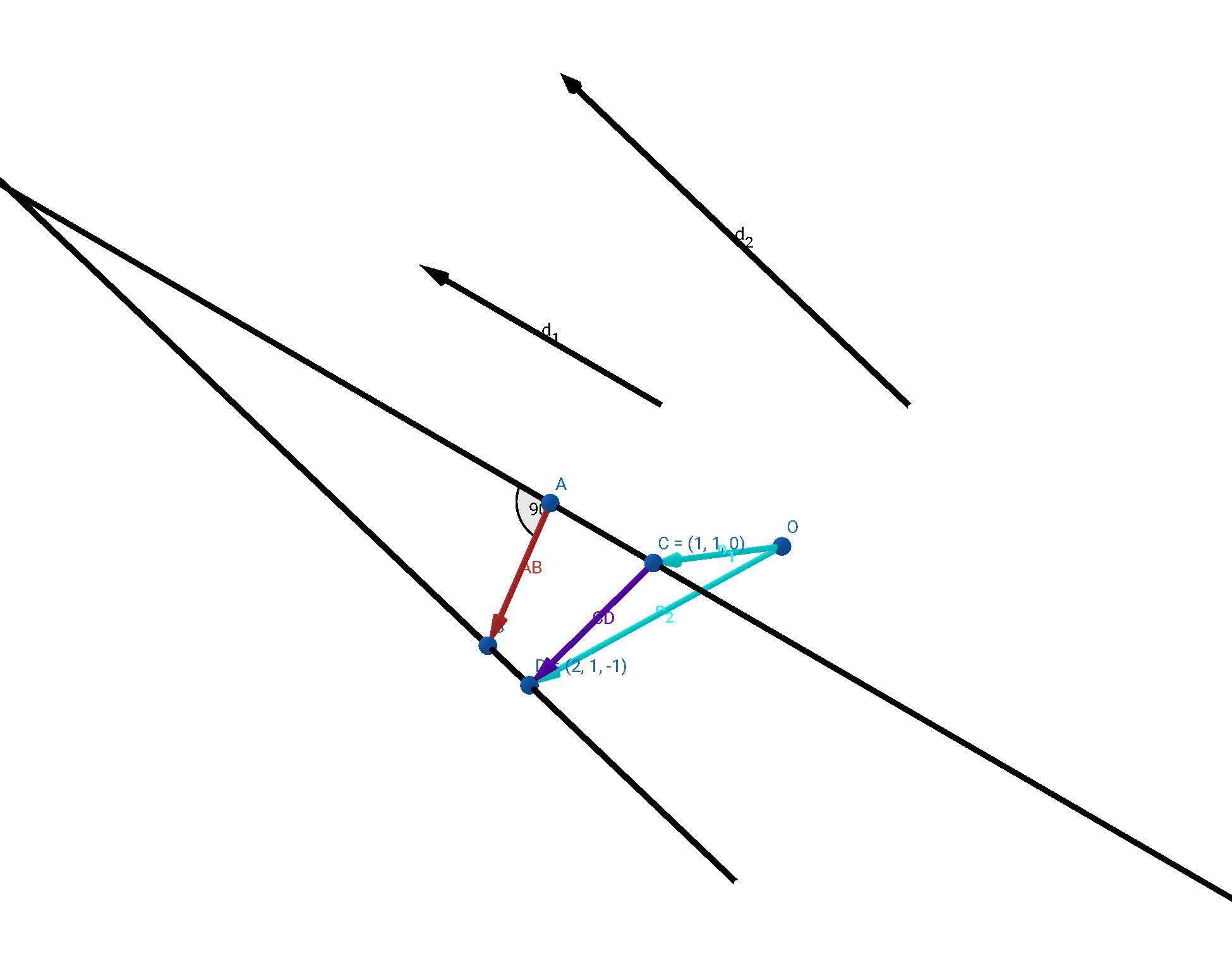
In the figure below, arrows $\overrightarrow{p_1}$ & $\overrightarrow{p_2}$ are position vectors of points C (1,1,0) & D (2,1,-1) on lines L1 & L2. The position vectors are shown by blue coloured arrows from origin O to points C & D. 

(I have kept the three coordinate axes hidden this time so that we are only looking at what we want to.)

Our aim is to find the shortest distance AB, highlighted in yellow colour in the picture above. But the shortest distance is a scalar quantity; how will the four given vectors help us find a scalar? 

Well, not exactly. The four given vectors help us find the magnitude of a vector along AB. This vector has the magnitude equal to the length of AB - the shortest distance - and direction either from A to B or from B to A. So we can call it $\overrightarrow{AB}$ or $\overrightarrow{BA}$ depending on which direction we choose it to be in. I will define it in the direction from A to B. 

So ultimately our goal is to find the magnitude of this new vector from given pairs of position and direction vectors. 

Now, the segment AB is perpendicular to line L1, and $\overrightarrow{d_1}$ is parallel to L1. So the vector along AB, $\overrightarrow{AB}$, is perpendicular to $\overrightarrow{d_1}$. 

Segment AB is perpendicular to Line L2 as well, and $\overrightarrow{d_2}$ is parallel to L2. So that means $vecAB$ is also perpendicular to $\overrightarrow{d_2}$. 

So it is clear that $\overrightarrow{AB}$ is perpendicular to both the direction vectors.

The cross product $\overrightarrow{d_1}\times \overrightarrow{d_2}$ is another vector that’s perpendicular to both $\overrightarrow{d_1}$ & $\overrightarrow{d_2}$. Hence, the cross product must be parallel to $\overrightarrow{AB}$. 

The cross product can be either parallel and in the same direction as $\overrightarrow{AB}$, or parallel but in the opposite direction of $\overrightarrow{AB}$. 

We could have also gone with $\overrightarrow{d_2}\times \overrightarrow{d_1}$ which is of the same magnitude as $\overrightarrow{d_1}\times \overrightarrow{d_2}$ but in the opposite direction. Any of the two cross products will work. 

We will need to define one more vector along the segment CD, but first we will put a segment between C and D if we haven’t done so before. CD is just any other path between the lines(not the shortest path) and its length is required to find the length of the shortest path AB. 

Now define $\overrightarrow{CD}$ or $\overrightarrow{DC}$. Again, any of them will work. I am going with $\overrightarrow{CD}$. We can easily find the length of segment CD, or the magnitude of $\overrightarrow{CD}$, from given position vectors using the triangle law of vector addition. 

$\overrightarrow{CD}=\overrightarrow{p_2}-\overrightarrow{p_1}=2\hat{i}+\hat{j}-\hat{k}-(\hat{i}+\hat{j}+0\hat{k})$

$\overrightarrow{CD}=\hat{i}-\hat{k}$

Magnitude of $\overrightarrow{CD}$ = $|\overrightarrow{CD}|$ = $\sqrt{2}$

We have done a lot of random pickings so far. We have a choice to go with either $\overrightarrow{AB}$ or $\overrightarrow{BA}$.....$\overrightarrow{p_2}-\overrightarrow{p_1}$($\overrightarrow{CD}$) or $\overrightarrow{p_1}-\overrightarrow{p_2}$($\overrightarrow{DC}$).....$\overrightarrow{d_2}\times \overrightarrow{d_1}$ or $\overrightarrow{d_1}\times \overrightarrow{d_2}$. 

It will not entirely be true if i tell you that different choices will not lead to different answers. Different choices WILL alter the answers but the difference will only be in the sign. Some choices will give us a positive value, while some will lead to the same value but with a negative sign before it. More on this later. 

Is there any relation between vectors $\overrightarrow{AB}$ & $\overrightarrow{CD}$ ? 

Yes, there is; we will be able to see that clearly if we draw two parallel planes, each containing one of the two skew lines. In my previous post on the topic I mentioned that for any pair skew lines there exists a unique pair of parallel planes, each containing one of the two lines. 

Drop the perpendicular from point C onto the parallel plane, let it meet the plane at point E. This perpendicular CE will have the same length as AB. Connecting E and D to form a right triangle. Let angle DCE be $\theta$. 

Here’s a gif image just in case….

(I have kept the position vectors and the origin O hidden for clarity purposes)

So cos $\theta$ = $\frac{CE}{CD}$

For CD, we can write $|\overrightarrow{CD}|$

So, CE = AB = $|\overrightarrow{CD}|$ cos $\theta$ …(1)

                     = $\sqrt{2}$ cos$\theta$

Now how do we find cos $\theta$?

The way we do it is by using the dot product formula for vectors. If we define $\overrightarrow{CE}$, then $\theta$ is the angle between vectors $\overrightarrow{CD}$ & $\overrightarrow{CE}$. But $\overrightarrow{CE}$ is parallel to $\overrightarrow{AB}$ which in turn is parallel to $\overrightarrow{d_1}\times \overrightarrow{d_2}$. 

So $\theta$ is also the angle between vectors $\overrightarrow{CD}$ and $\overrightarrow{d_1}\times \overrightarrow{d_2}$. Using the dot product formula, cosine of $\theta$ is equal to the dot product of these two vectors, divided by the magnitude of $\overrightarrow{CD}$ multiplied by the magnitude of $\overrightarrow{d_1}\times \overrightarrow{d_2}$. 

$cos\theta =\frac{\overrightarrow{CD}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})}{|\overrightarrow{CD}||\overrightarrow{d_1}\times \overrightarrow{d_2}|}$

Substituting for cos $\theta$ in equation (1), 

AB = $|\overrightarrow{CD}|$ cos$\theta$ 

= $|\overrightarrow{CD}|\frac{\overrightarrow{CD}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})}{|\overrightarrow{CD}||\overrightarrow{d_1}\times \overrightarrow{d_2}|}$       

Which further simplifies to, 

= $\frac{\overrightarrow{CD}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})}{|\overrightarrow{d_1}\times \overrightarrow{d_2}|}$ …(2)

$\overrightarrow{CD}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})=(1)(3)+(0)(-1)+(-1)(-7$

$=3-0+7$

$=10$

$|\overrightarrow{d_1}\times \overrightarrow{d_2}|=\sqrt{3^2+(-1{)}^2+(-7{)}^2}$

                                                                         $=\sqrt{9+1+49}$        

                                                                         $=\sqrt{59}$

                   

Hence,

Shortest distance between = AB  $=\frac{10}{\sqrt{59}}$ units

               L1 & L2         

 

Equation (2) is close to the standard formula found in many textbooks for the shortest distance between skew lines. Replacing $\overrightarrow{CD}$ with $\overrightarrow{p_2}-\overrightarrow{p_1}$ or $\overrightarrow{p_1}-\overrightarrow{p_2}$, whichever was your choice, to express the formula entirely in terms of the given parameters. 

Shortest distance = $\frac{\overrightarrow{p_2}-\overrightarrow{p_1}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})}{|\overrightarrow{d_1}\times \overrightarrow{d_2}|}$

        

Going back to the point i made earlier, for a certain choice of vectors we will end up getting negative final answer. For instance, if we would have taken the cross product $\overrightarrow{d_2}\times \overrightarrow{d_1}$ instead, the final answer would then be -$\frac{10}{\sqrt{59}}$. You can verify it yourself. 

We can use the line of reasoning that the distance cannot be negative, and simply discard the negative sign, as if it was never there. That’ll work. 

Textbooks solve this issue of negative sign by taking the absolute value of the entire term on the right hand side of the formula. 

Shortest distance = $|\frac{\overrightarrow{p_2}-\overrightarrow{p_1}\cdot (\overrightarrow{d_1}\times \overrightarrow{d_2})}{|\overrightarrow{d_1}\times \overrightarrow{d_2}|}|$

Regardless of whether the term is positive or negative, its absolute value will always be positive. This is an effective way to get rid of the negative sign!