Angles in the same segment of a circle are equal

In this post, I will show you a couple of ways to prove that angles in the same segment of a circle are equal. The statement seems a little mysterious but the proofs are quite simple. So before going into any of the proofs, I want to quickly clarify the meaning of some of the terms occurring in the statement for those of you to whom the statement doesn’t seem to make sense.

What is “segment” of a circle?

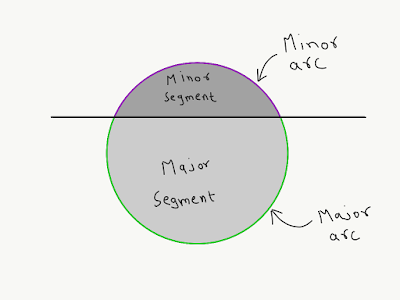
Given a circle, draw a line that cuts across the circle. This line divides the circle into two regions. These regions are what we refer to as “segments” of the circle.

The segment with the larger area is the major segment. The other segment of comparatively smaller area is the minor segment. The part of the borderline(circumference) of the circle that belongs to the major segment is the major arc, and the other part which belongs to the minor segment is the minor arc.

What do we mean by “angle in a segment” of a circle?

I will use letters P and Q to name the points where the line cuts the circle in the figure. Let A be any point on the minor arc, and B be any point on the major arc (These points can be anywhere on the respective arcs except where P and Q are).

Next up, I will connect points P and Q with A and B.

Angle PAQ is the angle subtended by the major arc, at point A on the minor arc, in the minor segment of the circle. This is what we are referring to as “angle in a segment”. Particularly, this is an angle in the minor segment subtended by the major arc.

Angle PBQ is the angle subtended by the minor arc, at point B on the major arc, in the major segment of the circle. This is an angle in the major segment of the circle subtended by the minor arc.

The theorem states that angles in the same segment of a circle are equal. So that basically means that the major arc subtends equal angles at all points on the minor arc. And the minor arc subtends equal angles at all points on the major arc.

Hopefully that makes sense. Now, let’s see the proof(s).

Proof 1 :

The first proof is pretty easy. It is actually a direct outcome of another standard theorem on circles. This theorem states that the angle subtended by an arc of a circle at the center is twice the angle the arc subtends at any other point on (the rest of) the circumference of the circle. The ‘rest of the circumference’ is actually nothing but the arc of the opposite segment!

We can restate the same thing the other way around for our convenience. That is, the angle subtended by an arc of a circle at any point on the (rest of the) circumference of the circle is half the angle it subtends at the center.

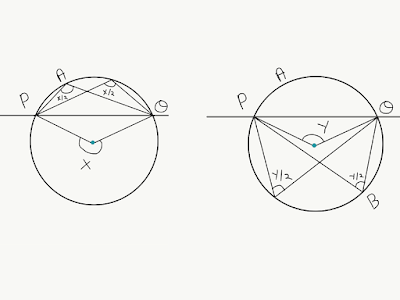
So in our figure, if the major arc PQ subtends angle X at the center, it will subtend angle \(\frac{X}{2}\) at every point on the minor arc, which is the remaining part of the circumference of the circle(see the far left figure). So that straightforwardly implies all angles in the minor segment are \(\frac{X}{2}\).

Similarly, if Y is the angle subtended by the minor arc at the center, then \(\frac{Y}{2}\) will be the angle it will subtend at every point on the major arc. Hence, all angles in the major segment are \(\frac{Y}{2}\).

Proof 2 :

The second proof feels to me like my own little invention because I couldn’t find this proof anywhere else I looked online! But nonetheless I still think it a simple and neat proof. Here we will use a property of cyclic quadrilaterals. Cyclic quadrilateral is a quadrilateral(four sided figure) whose four corners are on the circumference of the circle. Or simply, it is a quadrilateral inscribed in a circle. It has the property that both pairs of its opposite angles are supplementary(their sum is 180°).

Read : Opposite angles of a cyclic quadrilateral are supplementary.

Let \(\theta_1\) & \(\theta_2\) be any two angles in the minor segment of the circle as shown below, and let \(\theta_3\) & \(\theta_4\) be any two angles in the major segment of the circle.

Our aim is to prove, \(\theta_1\) = \(\theta_2\)

and \(\theta_3\) = \(\theta_4\)

In the figure to your left(or above), quadrilaterals APBQ, CPBQ, APDQ, CPDQ are cyclic quadrilaterals. In the image below, I have repeated the same figure 4 times to highlight each quadrilateral separately.

In each of the four cyclic quadrilaterals opposite interior angles are supplementary. So,