Angle Subtended by an arc at the center is twice the angle it subtends on the circumference

I will begin by clarifying the meaning of ‘angle subtended by an arc at a point’. 

An arc is any portion of the circumference(boundary) of the circle. Connecting the endpoints of an arc with the center of the circle results in the formation of the central angle by the arc.

This is what we are referring to as the angle subtended by an arc. Particularly, this is the angle subtended by an arc at the center of the circle, hence the name central angle. 

An important theorem on circles states that the central angle of an arc is twice the measure of the angle the arc subtends at any point on the remaining portion of the circumference of the circle. ‘Remaining portion of the circumference’ is just anywhere on the boundary of the circle except the arc in question.

In the figure, ABC is an arc, and D is a point on the (rest of the) circumference of the circle.

So if x is the angle subtended by arc ABC at (any) point D on the (rest of the) circumference, as per the theorem, the central angle AOC of arc ABC is 2x. 

It is convenient for me to just use the term ‘Circumference’ from here onwards instead of ‘Rest of the circumference’ everytime!

So, how do we prove this theorem? 

It is convenient for me to use the same figure in the proof as well. 

Given : Let ABC be an arc of a circle which subtends angle x at a point, say D, on the circumference. Connect endpoints A and C of the arc with the center O to form the central angle, angle AOC.

To prove : ∠AOC = 2x

It is not really clear initially from the figure where we should begin. There is no property or theorem or any rule that we can apply here that immediately comes to mind, at least it did not to me. 

Nothing seems to be relatable in the figure except when you look at the segments AO and CO. 

They are the radii of the circle, hence equal. If we join AC, we have an isosceles triangle OAC. A triangle is isosceles if 

two of its sides have the same length. In an isosceles triangle angles opposite to equal sides are also equal. So,

∠OAC = ∠OCA = y (say)

The third interior angle of triangle OAC will then be (180° - 2y), because the three interior angles of a triangle sum to 180°. Note that the third interior angle is the central angle of arc ABC. So basically (180° - 2y) is equal to 2x is what we want to prove. 

So what next? 

It seems like we have again hit a dead end. Maybe we need to do some more construction. O and D are the only points that are not connected in the figure. So let’s join O with D. 

Notice that OD is also the radius of the circle. This second bit of construction gives us two more isosceles triangles to work with. Triangle OAD and triangle OCD. 

Let ∠OCD be z. Since OC and OD are equal sides(radii), ∠ODC will also be z. The third interior angle, ∠COD will be (180° - 2z). Notice that ∠COD is the central angle of arc CD. Arc CD is highlighted in green in the figure. 

In triangle AOD, ∠ADO is (x - z).

Since OD and OA are equal sides(radii) ∠AOD will be (180° - 2(x - z)), which is the central angle of arc AD. 

Now, the three arcs, ABC, AD and CD together complete the circumference of the entire circle. Together they subtend 360° angle at the center. So all three central angles in our figure add up to 360°. 

(180° - 2(x - z)) + (180° - 2z) + (180° - 2y) = 360°

We will keep 180° - 2y as it is on the left hand side because that’s the central angle of arc ABC, which we want to prove to be equal to 2x.

180° - 2x + 2z + 180° - 2z + (180° - 2y) = 360°

We see the z terms cancel each other out on the left. 

180° - 2y = 360° - (180° + 180° - 2x)

180° - 2y = 360° - 360° + 2x 

               = 2x

So, ∠AOC = 180° - 2y = 2x

And so, this proves that the central angle of arc ABC is 2x. 

So it seems like we are done proving the statement : angle subtended by an arc at the center is twice the angle it subtends at a point on the (rest of the) circumference. But actually, we aren't quite done with it yet. 

You see in the figure above, the location of point D that we had (arbitrarily) chosen on the circumference is up above center O. We can also have D positioned somewhere to the right of center O, or to its left as shown in the figure below. 

This brings in slight modifications to the figure; it is not the same looking. Observe that now chord AD cuts through radius OC when D is to the right of center O, and chord CD cuts through radius AO when D is to the left of center O. The proof for these new configurations will look slightly different too. 

In a nutshell, for the position of D anywhere in the red region of the circumference in the figure, the proof is the same which we just saw. We are about to see the proof when D is in any of the two green regions of the circumference. 

There is also a third configuration at the borderline of green and red regions. Here, point D on the circumference is at the border of the two regions. In this third situation, chord AC overlaps radius OC or chord CD overlaps radius AO.  

This is the simplest of the three cases to prove. But first let’s see the proof when D is in one of the green regions of the circumference. 

The method used in the proof is similar, we are looking for isosceles triangles to begin with. 

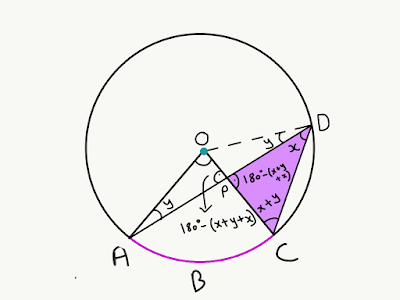
In the figure, chord AD cuts through radius OC at point P. Arc ABC subtends angle x at point D on the circumference. Again, we are proving ∠AOC = 2x, which is same as saying ∠AOP = 2x. 

The construction part of the theorem remains the same as in the above proof. Connect center O to point D. 

We have two isosceles triangles in the figure. Triangle OAD and triangle OCD. 

In the figure below, I have marked the two equal angles in the isosceles triangle OAD with letter y. 

We can say that the third interior angle, ∠AOD, measures 180° - 2y, but we do not require this angle in the proof. So I am not going to mark it in the figure. 

In triangle ODC, part of angle ODC is x and its other part is y. So the whole angle ODC is x + y. This angle is equal to angle OCD because the triangle is isosceles(OD = OC). 

Now let’s look at the small triangle PCD. Two of its interior angles are x and x + y, so the third interior angle will be 180° - (x + x + y). 

This angle is vertically opposite to ∠OPA which comes inside triangle OPA. Hence measure of angle OPA is also 180° - (x + x + y), which simplifies to 180° - 2x - y. 

Finally, in triangle AOP, two of the angles are y and 180° - 2x - y. So the third interior angle will be 180° - (y + (180 - 2x - y)). 

So, Angle AOP = 180° - y - (180° - 2x - y)

                         = 180° - y - 180° + 2x + y

                         = 2x

Hence proved. 

The proof for D in the other green region of the circumference is very similar to this proof. So i am going to save my time and jump directly to the last distinct configuration where point D is at the boundary of green and red regions. 

In the figure, chord CD overlaps the radius CO. D is now at the boundary of green and red regions of the circumference. 

Should we join O and D again in the figure?

Well, COD is a single straight line segment; O and D are already connected! We don’t need to do any construction here. We already have a premade isosceles triangle, triangle ODA. 

Two of its equal interior angles are x, hence the third interior angle will be 180° - 2x, as shown in the figure above. 

Points C, O and D are collinear. Therefore, angle AOC is 180° - (180° - 2x), which equals 2x. 

Hence proved! 

Here again, the proof for the case when chord AD is overlapping the radius AO is very much the same. So I am just going to skip that proof as well. 

We are still not done with all possible scenarios. There is still one more configuration left that we haven’t discussed, which has to do with the arc in question. Notice that ABC is a minor arc. It is minor because it is smaller than half the boundary(circumference) of the entire circle. But what if it was a major arc, bigger than half the boundary of the circle, as shown in figure below? 

If ABC is a major arc then it is not possible for chords CD and AD to intersect or overlap radii OA and OC. So for a major arc there is only one configuration, the proof of which is identical to the proof that we saw for the minor arc when D was in the red region of the circumference.

So I think we covered all possible scenarios, and with that we conclude that the angle subtended by an arc at the center is always twice the angle it subtends at any point on the (rest of the) circumference.