Ceva’s Theorem and its Converse(without proof)

Ceva’s Theorem is a fundamental theorem related to triangles. It was proved by an Italian mathematician Giovanni Ceva. Even though he may not have been the first to prove it, the theorem still bears his name. 

I will write about one of many(pdf file) proofs of Ceva’s theorem and its converse in some other related post. This post is all about understanding the patterns in the mathematical relation given by the theorem.

A cevian is a line segment joining a vertex of a triangle to any point on the line which contains the opposite side of the vertex. A cevian can lie outside of a triangle too, which we generally find in the case of obtuse angled triangles.

(NOTE : Is the line segment overlapping an edge of a triangle a cevian? I have attempted to answer this question at the end of this post.)

Sometimes a cevian is also defined as a line(instead of a segment) that passes through a vertex and cuts the line which contains the side opposite to the vertex. 

In △ABC in the figure below, AD, BE and CF are three cevians from the three vertices. They are all intersecting at a single common point. In other words, the cevians are concurrent. In △PQR, the three cevians from the three vertices are not concurrent. In △MNO, the three cevians from the three vertices are concurrent but the point of concurrency lies outside of the triangle, and it is obtained by extending all the three cevians(we can see now why defining a cevian as a line instead of a line segment works better in this case). 

If three cevians from the three vertices of a triangle are concurrent, then Ceva’s theorem says that, 

\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\).

All the terms we see in the three fractions above are directed segments. I will go into the details of this in a moment. But first, the Converse of this theorem. 

Converse of Ceva’s theorem is also true. It can be stated as : 

In △ABC, if AD, BE and CF are three cevians from the vertices A, B and C, meeting the opposite sides(or their extensions) at points D, E and F, and if, 

\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)  is true, 

then, the cevians AD, BE and CF are concurrent. 

The converse of Ceva’s theorem is a necessary and sufficient condition for the three cevians from the three vertices of a triangle to be concurrent. 

Now let’s peer into the finer details of the mathematical relation in the theorems. I will make an attempt to explain the pattern in which the terms(directed segments) in the three fractions are organised. First for an acute angled triangle ABC, 

Points A, F and B are on the line that contains the side AB. The first fraction is \(\frac{AF}{FB}\). In the numerator, we have the directed segment from vertex A to point F - the point where the cevian from C meets the line. In the denominator, we have the directed segment from F to the other vertex, B, on the line. 

Points B, D and C are on the line that contains the side BC. The second fraction is \(\frac{BD}{DC}\). It begins from the vertex B where the first fraction ends, and this is an important point to remember. In the numerator, the directed segment is from B to the point D  - the point where the cevian from the opposite vertex A meets the line. The denominator is the directed segment from D to the other vertex, C, on the line. 

Similarly, the third fraction begins from the vertex C where the second fraction ends. Here as well, first we are going from C to E - the point where the cevian meets the line, and then from E to the other vertex on the line, A. Also, the first fraction starts with A - the vertex where the third fraction ends. 

Ceva’s theorem says that the multiplication of these three fractions should be one if the cevians are concurrent, and vice-versa. 

\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)

For an obtuse angled triangle, the pattern is exactly the same. Let’s say we begin from vertex M on the line which contains the side MN. 

The first fraction is \(\frac{MZ}{ZN}\). We go from M to Z - the point where the cevian meets the line, and from Z to the other vertex N. The next fraction will begin from the vertex N on the line that contains the side NO. So again, from N to X - the point where the cevian from M meets the line, divided by the directed segment from X to the other vertex O.

So the other two fractions will be \(\frac{NX}{XO}\) & \(\frac{OY}{YM}\). And ceva’s theorem says that the product of the three fractions will be one if they are concurrent, and vice-versa. 

\(\frac{MZ}{ZN} \cdot \frac{NX}{XO} \cdot \frac{OY}{YM} = 1\)

As long as all the directed lengths are non-zero, we could begin the loop from any vertex or any directed segment. For example, in an acute angled triangle above, if we had initially started with the directed segment AE on the line that contains the side AC, the relation could then be written as : 

\(\frac{AE}{EC} \cdot \frac{CD}{DB} \cdot \frac{BF}{FA} = 1\)

which is the same as the relation written above. We have just inverted everything on the left hand and right hand sides, and switched the position of the terms from right to left. (If a = b, then \(\frac{1}{a} = \frac{1}{b}\) a, b \(\neq\) 0)

If we start from the directed segment BD on the line that contains BC, the relation will look like: 

\(\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1\)

which is again the exact same thing. This time we are just tweaking the position of the terms using associative and commutative laws of real numbers!  

(\(\frac{AF}{FB}) \cdot (\frac{BD}{DC} \cdot \frac{CE}{EA}) = 1\)...Associative Law of Real nos.

(\(\frac{BD}{DC} \cdot \frac{CE}{EA}) \cdot (\frac{AF}{FB}) = 1\)....Commutative Law 

\(\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1\)...Associative Law

It is important that we apply this pattern exactly as it is when we are using Ceva’s theorem. It would be wrong if we were to write it like this : 

\(\frac{AF}{FB} \cdot \frac{DC}{BD} \cdot \frac{CE}{EA} = 1\) ❌

The mistake is in the second fraction, the positions of DC and BD are swapped. This would only stand to be correct if we are outsidely given/know that \(\frac{BD}{DC} = \frac{DC}{BD}\), and that would only be true if AD is a median.

Ok. Let’s quickly look at a simple example. 

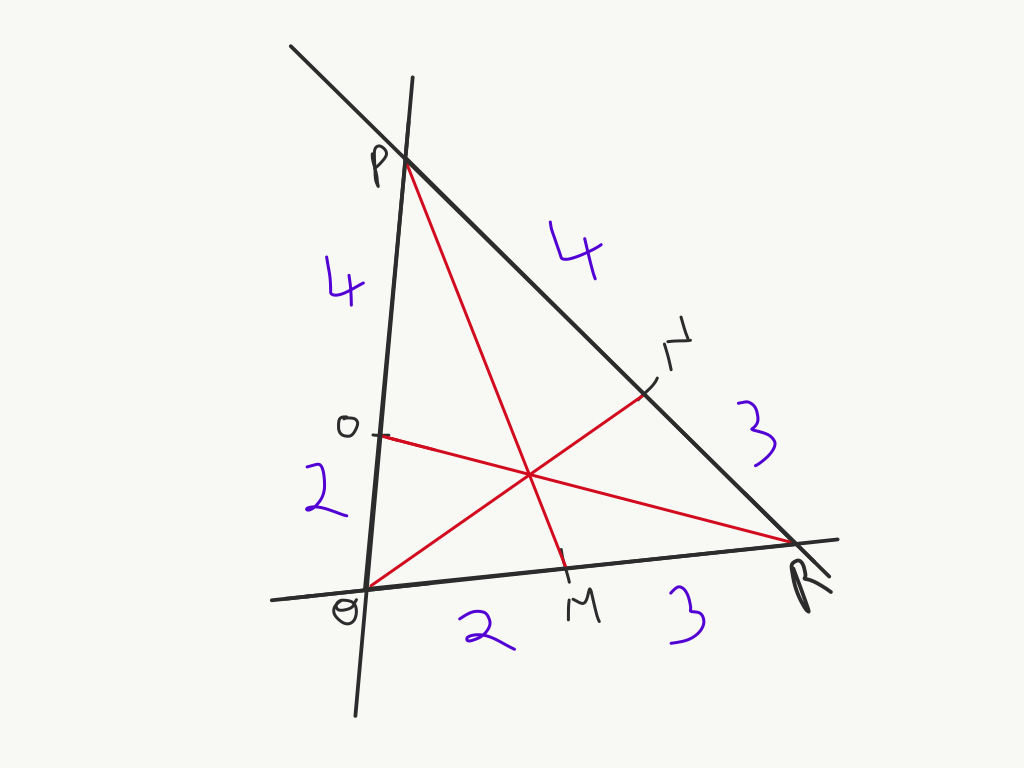
Points M, N and O divide the three sides of △PQR as shown in the figure below. 

If three cevians are drawn from the vertices P, Q and R to points M, N and O, then will they be concurrent? 

Here, we will use the converse of Ceva’s theorem to check the concurrency of the cevians PM, QN and RO. They will be concurrent if they satisfy the relation :

\(\frac{PO}{OQ} \cdot \frac{QM}{MR} \cdot \frac{RN}{NP} = 1\)

Substituting the values for the lengths of the directed segments as given in the figure, 

\(\frac{4}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} = 1\)

So yes, by converse of Ceva’s theorem, the cevians PM, QN and RO are concurrent. Notice that the direction aspect of directed segments is only important for writing the correct relation. After that they are all just lengths.

This was a pretty simple example. But we get to see the importance of Ceva’s theorem, and most importantly its converse, in examples where cevians are of some significance. For example, when the three cevians are the three medians of a triangle.

A median is the cevian connecting a vertex to the midpoint of the opposite side. There are a few ways to prove that the three medians of a triangle are concurrent. I have already shown one of those ways in my post about Medians and their point of concurrency - the Centroid. Proving this using the converse of Ceva’s theorem is probably the easiest way to do it.

We see in △ABC above, AD, BE and CF are the three median cevians from the three vertices. Since they are medians,

AF = FB    ;    BD = DC   ;   CE = EA             ……(1)

We will have to prove that :   

\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)

L.H.S. = \(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}\) 

From (1), 

            = \(\frac{AF}{AF} \cdot \frac{BD}{BD} \cdot \frac{CE}{CE}\)

            

= 1 = R.H.S.

Hence the three medians are concurrent by Converse of Ceva’s theorem. 

Similarly, using converse of Ceva’s Theorem, we could also prove the concurrency of three angle bisectors, and the concurrency of three altitude cevians(or just altitudes) of a triangle.  

Here’s a fun jigsaw puzzle on Ceva’s theorem i found online.

When I was writing this post a question kept bothering me everytime. A cevian can be inside a triangle or outside a triangle... but can it be ON a triangle? That is, can it be on an edge of a triangle? 

The simple answer is yes, it can, although Wikipedia disagrees with me. The issue here is, when a cevian is on a side of a triangle, one of the two directed segments on the opposite side of the vertex will be zero. In the figure below, AD is the cevian from vertex A overlapping the side AB. The directed segment BD on the opposite side is zero. 

If that directed segment happens to be present in the denominator of any fraction in the relation then we will have zero in the denominator which we don’t want. To overcome this issue, we write this relation a little differently.  

\(\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\)

\(AF \cdot BD \cdot CE = FB \cdot DC \cdot EA\)

We have the product of three directed segments on one side and the product of three directed segments on the other side. We use this new modified form of the relation to check the concurrency of cevians when one or more of them are coinciding on the sides of a triangle. 

Notice that in the above relation, if any directed segment is zero it would mean the entire left hand side or right hand side of the relation is zero. So for example, say BD = 0.

That means, \(0 = FB \cdot DC \cdot EA\)

which will be true only when atleast one of the three directed segments on the right hand side is also zero, which further implies that there should be one more cevian, other than AD, coinciding an edge of the triangle for this relation to satisfy, i.e. for the three cevians to be concurrent. And that other cevian has to be such that any one of FB, DC, EA is zero.

Here’s a familiar example under this. 

In a right angled triangle, two of the three altitude cevians coincide the two perpendicular edges of the triangle. In the figure below, the altitudes AD and CF from the vertices A and C overlap the two perpendicular sides AB and BC. So the two directed segments BD and FB on the sides opposite to the vertices A and C, are both zero. 

The two altitudes from A and C meet at the vertex B - the vertex where 90° angle is formed. And the third altitude is drawn from B. So it is easier to see that vertex B is the point where all three altitudes meet. We can simply conclude that the three altitudes of a right triangle are concurrent at the vertex of the right angle. Proof is not required for this simple case.

But still, if i were to use the converse of Ceva’s theorem to prove the same thing, we would have to show that :

\(AF \cdot BD \cdot CE = FB \cdot DC \cdot EA\)

BD = FB = 0, one of the three directed segments on each side is zero. 

So we get, 0 = 0 which is true

Hence by the converse of ceva’s theorem the altitudes of a right triangle are concurrent.

Here’s a post i found online which explains Ceva’s Theorem pretty well in a more fundamental way to what it actually is.